Marooned in Crater Lake by Alfred Powers
The Earth’s Curvature
BY J. W. BOOTH
“HOW was the real form of the earth found out? Brave and daring men left their homes, and traveled, without turning about, until they came to the very places they set out from. What does that prove?
It proves that the earth is round like a ball.
What other proof have we that the earth is round?
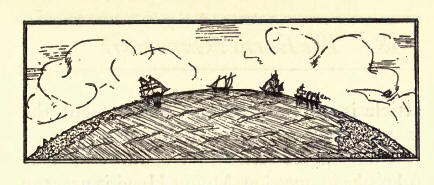
When a ship is coming in from sea, the tops of the masts are seen first, then the sails, then the hull.
Why does that prove that the earth is round?
Because if the surface of the water were flat, the hull would be seen as soon as the masts.”
–FROM AN OLD GEOGRAPHY.
IN the April number of the Improvement Era for the current year (1925), there is an article under the heading, “The Fourth of the Far Fifteen,” by Alfred Powers, the reading of which gives one a real thrill in Boy Scout work adventure and patriotism as well as an interesting lesson in the study of the rotundity of the earth and the problem in arithmetic of determining the curvature of this great globe on which we live. That article is well worthy of a place among the masterpieces of Boy Scout literature.
I have never seen either of those wonderful peaks in question. Mount Hood is near the northern border of Oregon and Mount Shasta, almost due south, is well over into the State of California, 250 miles away. They are near the meridian of 122 west longitude in the “utmost bounds of the everlasting hills,” and the writer of this is today at 37 east longitude in Aleppo, Syria, reading that fascinating challenge of the Hood River “Panthers” to the Klamath Falls “Pelicans” to scale the frozen heights of Shasta and receive, and answer, in “tongues of fire,” their night-time signals from the frosty summits of Mount Hood.
The Era lost not one jot of the interest so creditably concealed in its pages, even in its long postal journey of “half the convex world around,” and I am wondering if I can hold the interest of my readers in this simple tributary supplement to that very masterly article above mentioned.
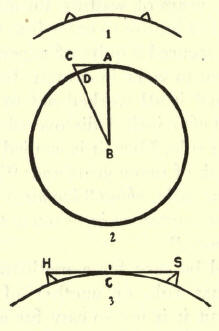
Before I had finished reading the second page, I stopped and asked myself if Mount Hood, 1 1,225 feet high, could be seen from Mount Shasta, 14,440 feet in altitude, with 250 miles stretching out between them. On a one-minute hasty calculation, I concluded it could not be seen 5 but a second and more studious thought, with the aid of a simple diagram, as is equal to Cut 1, a curved line with two projections, told me that one peak might be seen from the other on a clear day with a good glass. How did I come to make that mistake in my first calculation and then so easily correct it, all in less than five minutes? That is the interesting feature of this discussion and I want my Boy Scout friends to see how simple that problem is of measuring the curvature of the earth.
Now, when I was a boy at school, I was conspicuously noted for not being noted for anything in particular, and least of many things was I noted for being a mathematician. My brothers, John E. Booth and A. L. Booth of Provo, were both well up in that branch of science, and, though they did their best to get me to “see the point,” they finally concluded that I was a better absorber of their sympathy than of their lesson in science.
One day, A. L. made a casual remark about the “curvature of the earth.” Immediately, I was anxious to know how to work such an example, but, right there and then, I made up my mind to discover the method myself. I supposed, of course, it could be worked by trigonometry or calculus or mensuration. I was not even ankle-deep in algebra nor acquainted with the angles of plain geometry, yet I decided I would learn, without text book or teacher, how to calculate the curve of this big ball of land and sea whose surface area is equal to two hundred millions of square miles. I thought about it but would not talk to anyone on the subject lest I should get an idea not strictly original. I reflected, but refused to read about it, so anxious was I to learn it myself.
After 1 6 years of waiting for an uninterrupted spell of leisure to delve into my hobby problem, I secured a quire of paper and pencils and went to work in earnest. In less than a week I had it all worked out to the hundredth part of an inch. I discovered and wrote out my own rule. Here it is, copied from my old note book of many years ago:“The earth curves in one mile, about 8 inches, or .6636 + feet, and the curvature Increases as the square of the distance”
It would be easy for a mathematician to discover that rule or another of his own wording, but it is not so easy for a boy who doesn’t know how. The joy of discovery was well worth the time spent on it. All I used was simple eighth-grade arithmetic. If you don’t want to spend so much time in learning how to work the problem, just look at Cut 2 and you will have it in less than 1 minutes. You know that the square of the longest side of a right-angled triangle is equal to the sum of the squares of the other two sides.
Then, wherein was I mistaken in my first conclusion that one of these peaks in question could not be seen from the summit of the other? I was mistaken. They can be seen and the boys have demonstrated it.
Let the circle represent the circumference of the earth. A B the radius of 4,000 miles, nearly, AC the distance from point at sea level to the summit of a peak, say, 500 miles away. Now, D B is equal to A B, being radii of the same circle. The square of A B plus the square of A C equals the square of C B and, since that is true, it follows that the square root of the sum of the two shorter sides must be equal to the square root of the square of the long side, and the difference between the square root of the long side and the square root of the radius of the circle would equal the height of the peak. And it is clearly seen that a light could not be observed at A from any point lower than the summit C, 500 miles away. So when I read that it is 250 miles from Mount Hood to Mount Shasta, I said: “The square of 250 is 62,500, which multiplied by .6636 + gives us 41,475 feet, and a light less elevated than that could not be seen from a sea level point 250 miles distant” The combined altitude of Mount Hood, 11,- 225, and Mount Shasta, 14,440, as given in the article, would be only 25,665 feet, so that a light even of sun brilliance on the top of Mount Hood, with Hood on the top of Mount Shasta, could not have been seen 250 miles away, from sea level. Old Everest, nearly 30,000 feet high, with Mount Hood on top of it, could scarcely be seen from a ship in the Indian Ocean, 250 miles to the south.
Now, a glance at Cut 3 will convince the reader that if a light at C could be seen from both peaks, H and S, at once, then a fire at the summit of each of them could be seen from the other peak. If H and S were of equal altitudes, then their summits would be visible from each other at a distance just twice as great as that from which a light, as at C, could be seen from either peak. But Mount Shasta is 14,440 feet high and, calculating conversely, we find the square root of 14,440 (a number which multiplied by itself makes 14,440 + ) or 120+, and this divided by .6636-f-, the curvature for one mile, equals 1 80 miles, a distance from which, at sea level, that peak could be seen. Likewise, Mount Hood, 11,225 feet high, the square root of which is practically 106, divided by .6636, would give us 159 miles. This total distance then, 180 miles plus 159, is 339 miles, and were there only open sea level between them the two peaks could display their red lights one to the other even though they were 339 miles apart.
Looming up thousands of feet in the Cascade Range, between Mount Hood and Mount Shasta, and only a trifle out of direct line, are Mount Jefferson, The Three Sisters, Diamond Peak, Mount Thielsen, Mount McLaughlin and others, almost any one of which had it been at mid-distance and in direct line of light, would have kept the rays of Shasta’s red fire from the eager eyes of the boys on Mount Hood on that night of July 4th, at 10:30 P. M.
Now, Boy Scouts, after I have given you this one peep into the method of measuring the rotundity of the earth, let me give you an example for practice.
You are on a mountain 10,000 feet high. From the top of this you can see to the north a peak 100 miles away. To the east is one 50 miles away. Another to the south 60 miles distant, and the fourth to the west 40 miles away from you. You have a true spirit level with you, and, whichever way you test it, you see that the summit of each peak is on a dead level with that from which you take your measurements. What is the altitude of each of the four peaks?
The Teton Peaks Council of Boy Scouts ot America have recently sent me some interesting letters and literature from which I am getting some splendid lessons to hand over to some of the boys and girls of Syria. Any of that famous “Fifteen” of Hood River or Klamath Falls who happen to read this article, will favor us if they send personal letters with their greetings to the boys of the Near East. Tell me if I have missed my calculation on your wonderful giants of the Cascades, even with the natural curvature of half the world between us.
Aleppo, Syria,
May 15, 1925.
J. W. Booth, the missionary with an eager and youthful spirit who wrote this article, died in Syria in 1928. The article is published with the kind permission of The Improvement Era, Salt Lake.
***previous*** — ***next***
